2017大阪大学物理入試問題について

出題ミスとか採点ミスとか騒がれている入試問題について，普通の解法と，高校課程の範囲外になりますが，理論的に正しい解法を示します。

入試問題

　音叉を固定壁の近くに置き，壁からの反射音を利用してみよう。図のように，壁面に垂直にとった$y$軸に沿って音叉を移動させる。また，壁から遠く離れた$y$軸上の位置にマイクロフォンを固定する。マイクロフォンは，音叉から直接達する音と壁からの反射音を観測する。この実験では，音叉は十分小さく，点音源と見なせる。

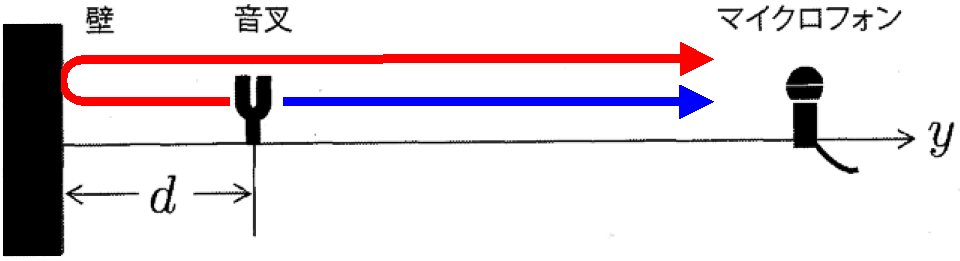
問4　$y$軸の正の方向に音叉の位置を少しずつ変えながらマイクロフォンで観測すると，音の強さが周期的に変動した。マイクロフォンで観測された音が強くなるときの，音叉と壁の間の距離$d$と音の波長$\lambda$との関係を表せ。必要であれば，自然数として$n$（$n=$1，2，3，…）を用いてよい。

普通の解法

もし固定端反射でなければ，強め合う条件は，行路差が単純に波長の整数倍で$2d=n\lambda$ですが，固定端であることを考慮することになります。阪大も，上記の解答を当初の正答としています。

高校レベルの扱いとしては，このへんが限界でしょう。たとえば小学校では，円周率は3.14で構いません。でも，これは，近似解で不正確なので，中学以降は$\pi$で表記します。それと同じで，高校程度で上記の扱いができれば，まあ，勉強したということは，評価できるでしょう。

正しい解答

これに対し，阪大は新たに$2d=n\lambda$，および$2d=(n-1)\lambda$を追加しています。

縦波である疎密波が強め合う条件は，基本的に範囲外になります。なので，過去の全国の入試出題例でも，音波の干渉に関する入試問題は，「ドップラー効果」「気柱の振動」「反射なしの直接音」に概ね限られています。

本問を正しく解くには，縦波の性質に着目する必要があります。直感的に把握するのは難しいので，いちおう数式を用いて記述します。数式自体は，高校生でも理解できるはずです。

音叉の位置を原点とし，右向きを$y$の正の向き，音速を$v$，振動数を$f$，振幅を$A$とする。
右向きに進む音波の原点における変位を，右向きを正として，$w_1(0)=A\sin(2\pi ft)$とする。
左向きに進む波は，$w_1(0)$と左右対称の変位を示すから，$w_2(0)=-A\sin(2\pi ft)$となる。
壁の位置$y=-d$における$w_2$の変位は$w_2(-d)=-A\sin\left\{2\pi f\left(t-\dfrac{d}{v}\right)\right\}$
反射波$w_3(-d)$は，$w_2(-d)+w_3(-d)=0$より，$w_3(-d)=A\sin\left\{2\pi f\left(t-\dfrac{d}{v}\right)\right\}$
これが右に進んで原点に到達するときの変位は，
$w_3(0)=A\sin\left\{2\pi f\left(t-\dfrac{d}{v}-\dfrac{d}{v}\right)\right\}$ $=A\sin\left\{2\pi f\left(t-\dfrac{2d}{v}\right)\right\}$
これと$w_1$の合成波は
$w_1(0)+w_3(0)=A\sin(2\pi ft)+A\sin\left\{2\pi f\left(t-\dfrac{2d}{v}\right)\right\}$
$=2A\sin\left[\dfrac{1}{2}\left\{2\pi ft+2\pi f\left(t-\dfrac{2d}{v}\right)\right\}\right]\cos\left[\dfrac{1}{2}\left\{2\pi ft-2\pi f\left(t-\dfrac{2d}{v}\right)\right\}\right]$
$=2A\sin\left\{2\pi f\left(t-\dfrac{d}{v}\right)\right\}\cos\left(2\pi f\cdot\dfrac{d}{v}\right)$
この合成波の振幅を最大にするには，$\cos\left(2\pi f\cdot\dfrac{d}{v}\right)=\pm 1$とすればよいから，整数$n$（$n=$1，2，3，…）を用いて
$2\pi f\cdot\dfrac{d}{v}=2\pi \cdot\dfrac{d}{\lambda}=n\pi$　よって$\underline{~~2d=n\lambda~~}$

従って，阪大が後から追加した正答が，理論的に正しい解答となります。

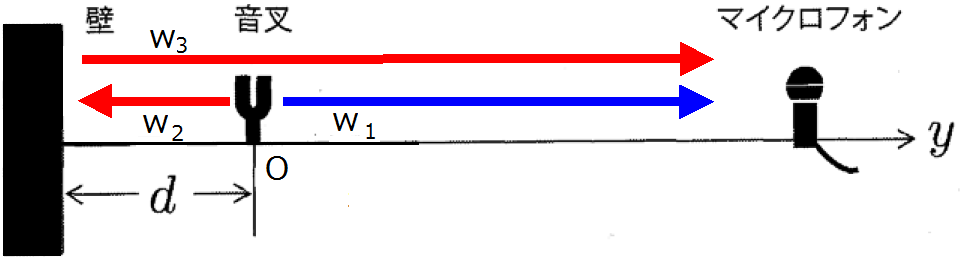
この問題のポイントは，縦波の場合，右へ行った場合と左に行った場合とで，変位が逆なことです。

横波であれば，発生してからたとえば0.1秒後の変位は，右へいった波も，左へいった波も，同じです。でも，縦波の場合，左右逆なのです。

一方，密度に注目すれば，密度は右にいく波も，左にいく波も，同じ時刻には同じ値をとります。また壁で反射するときには，密度は何ら障害されないので，自由端反射と見てよいです。ですから，単純に，$2d=n\lambda$がすぐに出てきます。

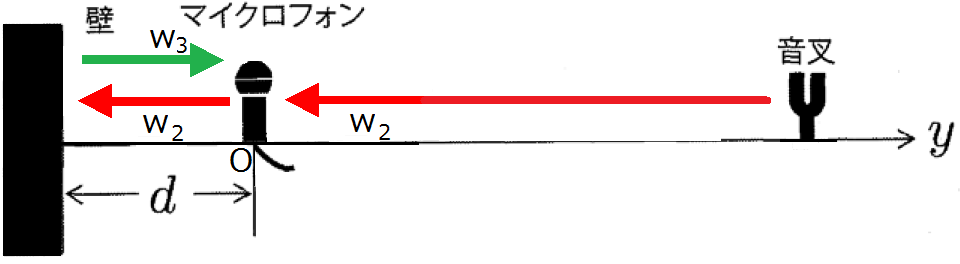
ただ，こういう考え方をすること自体，高校範囲外です。しかも，密度で考える場合，同じ方向に進む波と，反対方向に進む波では，強め合う条件が変わってきますから注意が必要です。たとえば，本問で，以下の図のように音源とマイクの位置が逆だと，条件は$2d=\left(n+\dfrac{1}{2}\right)\lambda$になります（興味のある人は理由を考えてみましょう）。

新正答の$2d=(n-1)\lambda$については，問題文中で$n=$1，2，3，… と置いたために，$d=0$の場合を考慮したものですが，$d=0$のときにはそもそも左へいく波$w_2$が発生しませんし，反射波も発生しませんから，干渉による振幅増大はありません。振幅はオリジナル音源$w_1$と同じです。この場合，「音が強くなるときの」という問題文に合いませんから，除外してもいいのではないかと思います。

なので，$2d=(n-1)\lambda$については，正答の範囲を限界まで広げるために，追加したものと思われます。

コメント

すぐにわかるように，「普通の解答」を超えるような考察が，限られた試験時間内でできる受験生はいません。いたとしても，阪大医学部を再受験した，国立大学物理学科出身者くらいでしょう。そして，「普通の解答」と同じ答えを書いた人は，はじめから正解とされています。

だから，この問題を放置し続けた阪大や文科省を責める気にはなれません。ネットでは，阪大や文科省に対する攻撃が酷いですが，責任範囲としては，せいぜい，以下の程度でしょう。

• 厳密解を出すには高校範囲を超えるような問題を出題した
• 過去の出題例を調べなかった
• 入試時間内に厳密解を出すような「あり得ない受験生」を，採点のときに切り捨てた

とはいえ，実害が発生したとは到底思えないようなミスです。それでも公表した阪大は，きちんと運営されているということではないでしょうか。

ただ，言えるのは，同タイプの問題は，他大学では出題例が，ざっと見たところ皆無だということです。その点では，過去の出題例に基づき，それを微妙にひねってくる東大などとは異なり，リスキーな試みだったということは言えるでしょう。

音波は，なにかと問題が起きやすいジャンルです。

1980年代の後半頃，中学入試で駒場東邦中学が，ドップラー効果まがいの出題をしたときには，若干，中学受験塾が騒然としました。

そのときに，当時の国内トップの塾T（Sピックスの前身）でバイトしていた私は，専任講師から，その問題を数式化しろといわれて，困った経験があります。範囲外とはいえ，直感的には簡単な問題なのですが，小学生にわかるような形では，なかなか式で表現できないからです。

そういった一連の受験事情には，大学の出題者は，全く無頓着です。

現在，トップレベル進学校でも，中学入試問題や高校入試問題を作る先生方は，過去の出題例に忠実に作っています。

そもそも，新機軸問題を出せるほど専門の学問をやった先生は皆無だし，東大に多数の合格者を出す高校でも，その先生が東大入試問題をきちんと理解しているとは言えないことは，皆さんもご存知でしょう。

大学も，まさに，そういう状況になっています。東大ですら，独法化の影響で予算が限られてきたため，トップ層は企業に脱出するようになり，大学に残るのは，他大学出身の，大学院から東大に来た，東大入試とは無縁の人たちです。大学の講義を維持するには，他大学出身者や，専門外の非常勤をかき集めるしかないのです。

これを，当学院では，「大学の高校化」と勝手に呼んでいるわけですが，そういった場合には，過去の出題例に忠実に作問する必要がある，ということは言えるのではないでしょうか。

阪大は，さらにチェックをしっかりする，というようなコメントを出していますが，実際には，中学や高校の出題担当者がやっているような前例踏襲に，大学も習うことで，良問を出題することができるのではないかと思います。

そんな，「日替わりワンポイントアドバイス」でいつも書いているようなことが，確認されたような事件ではありました。

2018年1月8日　© 東京凰籃学院

大学受験アドバイスのコーナー