2004年数学第１問へのコメント

東京凰籃学院

東大数学第１問へのコメント

基本と応用の間には？

　2004年度文理共通第１問です。

　問題集などによりますと，この問題，けっこう難しいということになっているようです。たしかに解法はいろいろ考えられるのですが，どの方向で行っても計算量が多く，また一歩踏み外すと泥沼にはまる，というのです。

　この問題に，５分足らずで解ける驚異的（？）に簡単な解法がある，と聞いたら信じられますか？

　そのまえに，問題集等に掲載されている解き方としてポピュラーなものは次のとおりです。

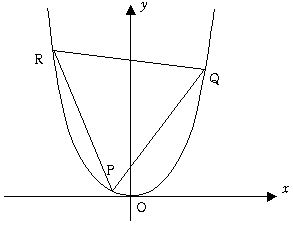
（１）P，Qの座標を設定して線分PQをPの周りに60度回転しRを表現する解法

　回転の方法としては，

　　ａ　複素数を用いる
　　ｂ　tanの加法定理を用いる

　が考えられ，またRの扱い方として，

　　ｃ　放物線上にある条件を用いる
　　ｄ　三辺PQ，QR，RPの傾きを用いる

　が考えられます。

（２）PQの垂直二等分線と放物線の交点がRであると置く解法

　Rの条件の出し方としては，

　　ｅ　PQの中点Mを起点とするベクトルMRを考える
　　ｆ　素直に垂直二等分線を求める

　といった方法が考えられます。

　各自問題集を見てみてください。

　ところで試験場では，特殊な解き方をして失敗することを恐れる心理が働き，まず無難な解き方から試そうとするものです。ですから，多くの受験生は最もシンプルな座標幾何，すなわちｆの解法を最初に試みたのではないでしょうか。

　と思ったので，解答速報ではｆの解き方を掲載しました。この解法では，ベクトルも複素数も三角関数も全く使っていません。試験場で思いつきやすく，また強引にでも解答を出してしまいたい，という，実戦的な解法といってもいいかもしれません。

　ただし，これらの解法はいずれもかなりの計算を要します。多くの受験生が計算の途中で断念したことでしょう。

　ところで，例の「驚異の（？）解法」です。

　受験生でこれを試みた人がいないかどうか聞いてみたのですが，聞いた範囲ではどういうわけか全くいません。既に2004年度東大入試問題の解答もいろいろ出版されて出回っていますが，この解法を掲載しているものが全く見あたりません。もちろん，なにぶんにも出版物はたくさんありますから，中には掲載しているものもあるかもしれませんが，とりあえず今のところ容易には発見できません。そんな事情もあって，この解法は思いつきにくいのかな？と思い，今まで掲載しなかったのですが，実は「教育的に考えて」，最初に思い浮かんでもいいのではないかと思うのです。

　解法は以下の通りです。

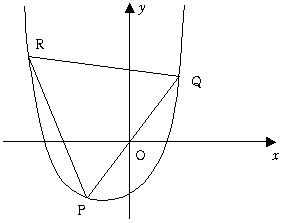　この解法に従えば，計算量は極めて少なく，計算の中味も高校入試レベルです。計算用紙もほとんど消費しません。

　ポイントは，放物線そのものを平行移動してしまうことです。なぜこんなことを思いつくかというと，この問題の難しさの本質は，

対称性の欠如

だからです。それで，できるだけ対称性よくパラメータをおこう，と考えるわけです。

　そもそもパラメータ（上の解答ではt）というのは，がむしゃらにおけばいいのではなく，対称的に設定して数を減らすのが基本なのです。ですから，PとQの座標を別の文字で置くという方法は得策ではありません。もちろん座標表示用の文字数を減らした分，放物線の式の未定係数が出てくるのですが，こういった場合，対称性をとったメリットのほうが上回ります。

　そしてもう一つ，教育的視点から見てみましょう。基本的な問題集なら必ずといっていいほど，

○　放物線を平行移動した式を求める
○　三点を通る放物線の式を求める

といった問題が出ているはずです。東大受験生なら必ずどこかでやったことがあるでしょう。こういう基本に習熟していれば，放物線の式に座標を代入して係数を決定するというきわめて原始的な方法がすっと出てくるのではないでしょうか。「東大入試ではセンスが求められる」とよく言われますが，それは，おそらくこういうことなのです。もちろんこの問題では，一般的な解法をとって，計算力で押し切るのも「あり」です。パワーか発想，どちらかがあれば解けるようになっています。

　パワーで行くにしてもセンスで行くにしても，基本問題を何度も繰り返して習熟することが合格への近道です。たしかに基本を積み上げるのは根気が要りますし，ときにはそれを単なる詰め込み教育などと言って非難したくなるかもしれません。そういうときは，基本問題の意義を考えましょう。数学の問題の解法を考えて楽しめるようになるために，基礎練習が不可欠なのだと考え，期待感をもって乗り切ってほしいと思います。

　逆に最初から「おもしろそうな」応用問題を追いかけてばかりいると，やがて壁に当たり，上達できないつらさを味わうことになります。

　基本練習は大変で，その精神的苦痛が受験のネックになるわけですから，基本の意義や重要性をたえず確認できるような環境に身を置いて，学習を加速するのが最良の道です。

　受験生の皆さんのご健闘を祈ります。

2004年7月5日

「大学受験アドヴァイスのコーナー」目次に戻る