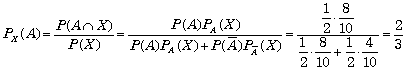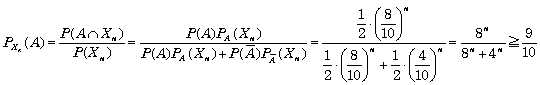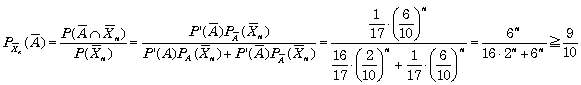スタッフルームから 「過去」を占う? 変な確率 〜授業〔東大文系/理系数学〕からのこぼれ話〜 |
 |
以下に確率論の話が出てきますが,高校課程の範囲で話を進めます。最新の統計学ではもっといい(と思われる)計算方法がありますが,とりあえずそういうことでご了承下さい。また,数式を扱うのが本題ではないので,数学アレルギーの人もご心配なく。
確率というのは,普通「未来」を占うために使われる。天気予報しかり,合格可能性判定しかり……。しかし,「条件付き確率」の単元では「過去」を占うとしか思えないような奇怪な問題が出題される。もちろん,条件付き確率の「条件」とは時間の前後に関係ない概念なのだが,実際問題として,過去に起こった事柄の確率を扱うことが多い。
たとえば次のような例題がある。授業で実際に扱った問題とは聞き方が異なるが,内容はほぼ同一である。もちろん,フィクションである。
J国には怪しい隣国があり,密かに核弾頭を搭載した長距離ミサイルの開発を行っているという噂がある。これをR国としよう。このような噂が流れる背景には,A国のある軍事技術がR国に漏洩した疑いがあることがあげられる。この技術を知り得れば,当該ミサイルの開発において圧倒的に有利になる。当然,R国が技術を知っているのと知らないのとでは,J国の国家安全保障に大きな相違が出る。 A国の提供してくれたデータによると,世界各地のこれまでの実験結果から見て,技術を知っていれば開発国の現在の技術水準を問わず成功率は80%だが,知らなければ成功率は40%に低下するということである。 ここで,R国が技術を知っている事象をA,実験が成功する事象をXとする。はじめR国が技術を知っているかどうかは全くわからないから, J国政府は国防上,R国が技術を入手しているかどうか知りたい。しかし知る手段は限られており,その数少ない機会がR国の行うミサイル発射実験である。 いま,R国がミサイル発射実験を強行した。ミサイルが J国を越え,その領海に達したことから,この実験は成功と見てよいとする。 (1) R国が既に技術を入手している確率はいかほどか。 (2) R国が既に技術を入手していると判断されるには,実験を続けて何回成功させなければならないか。 (3) (2)の回数だけ実験が続けて成功したとする。だがこの後,R国の実験は失敗が続いた。何回実験が続けて失敗すると,R国が実は技術を知らないと判断されるか。 ただし,ここで「判断される」とは,「90%以上の確率があること」を指すとする。 |
ご覧の通り,「技術漏洩が過去にあったか否か」が問題になっている。もう確定してしまった過去を占うなど変な話だが,実際問題として,「わからないこと」を判断するには確率によるしかない。ここで面白いのは,確定済みの過去であっても,それを知らない者にとっては未だ確定していない,ということである。
入試が終わってから合格発表までの期間は合否が非常に気になる。受験生の中には,この期間が異常に長く感じる人もいるかもしれない。ところで,この時期には既に合否は決まっている。なるようにしかならない。だから,あとは天命を待つのみだ。だが,合格を祈りながら待つ人もいる。答案を再現して,合否を占おうとする人もいる。確定した「過去」が変わるはずもないのに……。
突然身内の者が交通事故に遭い,病院に運ばれたと電話がかかる。病院に向かう車の中で,怪我が軽いものであることを祈る。どの程度の怪我かは既に確定しており,無神論者に言わせれば,祈ったところで予後も変わらないというのに……。
およそ科学的とはいえないが,これが人間の心理というものだ。
確定済みの過去,知り得ない過去を祈ったり占ったりするのは確かに科学的ではない。にもかかわらず,上の例題のように,それが必要なことがある。ここで登場するのが確率なのだ。確率論が非科学的なのではなくて,人間が確率を用いようとする事情……計算の対象や動機そのものが非科学的なのである。
上の解答らしきものを示しておこう。公式に従うだけなので詳しくは解説しないが,了承されたい。
| 条件より (1) (2) n
回続けて実験が成功する事象を
より, (3)
より, |
ところで授業では,
(3)で,P'(A)=16/17 というものが出てくるが,問題文には PP(A)=1/2 とあるではないか,どうしてこれを用いないのか?
という質問が出たが,これこそこの確率の不可解さを物語っている。問題文では情報漏洩があったか「全くわからない」ので確率は半々と設定されている。だが,(3)では既に4回の実験が行われて,新しい情報が得られているので,初期値として使う確率が異なるのである。上の質問の回答としては,ひとまずこれでいいだろう。
では,当初は本当に「全くわからなかった」のか? こう問われると,問題の設定だからとしか言いようがない。しかし現実社会では何らかの情報が他に得られているはずである。その情報に基づいて初期値を決めればよい。ところで,その初期値は具体的にどうやって決めるのか? 最初に得られている「情報」は計量可能なのか? もしそうだとして,初期値はどの程度正確に決まるのか?
ここにいくらでも不確定要素が入りうる。初期値がいい加減なら,それをもとにして求めた確率もまたいい加減なものではないのか? 上の質問にはそのような問題意識までもが含まれているに違いない。
このような奇怪な事態になるのは,確率論がいい加減だからというよりむしろ,これをわけのわからない現象に無理矢理適用しようという人間側の動機にある。
数学は,それが理科系の計量空間で用いられている限りは,きわめて美しい整合性と正確さ,客観性を誇る。ところが,応用数学,特に心理,政治,経済など,人文科学の分野で用いられる場合には,おそろしく恣意的な結果になりかねないのだ。統計がどこか怪しいと言われ続ける理由もそこにある。
文系の諸君もこれからはいろいろな場面で数学に出会い,数式を使うことになると思うが,その適用方法や限界については,理系の人間に劣らず慎重になる必要がある。くれぐれも数式に粉飾された怪しいデータに騙されることなく,データ作成者の動機にまで踏み込んだ理解を心がけてほしい。